Title

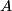
The singular value decomposition of a matrix is defined as

$\begin{displaymath} A = U \Sigma V^H \end{displaymath}$

(1)

where

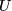
and

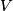
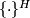
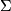
are both matrices with orthonormal columns, $\{\cdot\}^H$ indicates a complex-conjugate transpose, and $\Sigma$ is a diagonal matrix with singular values

$\sigma_1 &gt; \sigma_2 &gt; \cdots &gt; \sigma_n \geq 0$

along the main diagonal. Eq. (1) is just one of the many matrix decompositions that exists for matrix

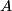
-- TWiki Admin User - 2016-02-16

Comments

Topic revision: r2 - 2016-02-19 - TWikiGuest