Metadata Repository
On this page:
Motivation
- If you have hundreds or thousands of webs on a TWiki site, web metadata stored in a data repository is useful.
- It can make things more efficient. For example, you can get the list of webs without traversing a directory hierarchy.
- It can make things otherwise impossible possible. For example, you can have metadata of a web which is not suitable to put on WebPreferences.
- If you run a federation of TWiki sites (detail later), each site needs to have site metadata of the others.
- Provided that you need to handle both site and web metadata, a uniform manner to handle those is handy.
- There are cases where other kinds of metadata needs to be handled.
Basics
It's optional
The repository being for a large site having hundreds or thousands of webs, its use is optional. It's activated only if the site owner explicitly turns on the metadata repository.Structure
- The repository houses data tables such as the site metadata table and the web metadata table.
- A table consists of records which have unique names. A web metadata record is named by the web name.
- A record consists of fields, each of which consists of a field name and a value. A field name is unique in a record and a field value is a string.
Only for top level webs
For practicality, web metadata is only for top level webs. More accurately, a subweb has the same web metadata as its parent. The reason is that site administration gets complicated if subwebs can have different web metadata.Examples
Here's how a metadata repository would be used by federated TWiki sites.Federation of sites
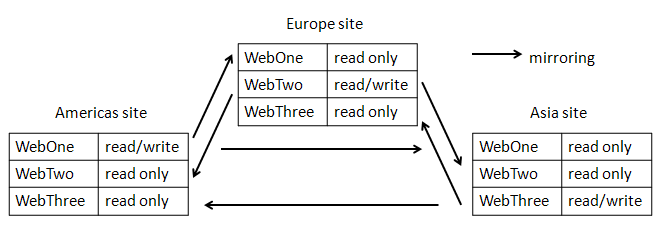
Let's assume the following federation of TWiki sites.- It consists of three TWiki sites - in Americas, Europe, and Asia.
- All sites in the federation have the same set of webs.
- Each web in the federation has one master site where update happens. This means that a web is read-only on a non master site.
- Let's say WebOne's master is Americas site, WebTwo's Europe, and WebThree's Asia.
- Each site mirrors sites whose master is not local periodically.
- Americas site mirrors WebTwo and WebThree.
- Europe site mirrors WebOne and WebThree.
- Asia site mirrors WebOne and WebTwo.
- Mirroring is basically copying files using the
rsynccommand.
Web admins
If there are many webs, it may not be easy to get hold of people responsible for a web. So it's handy if all webs have their admins clearly defined. Given that, let's assume we define admins for each web and store as a part of web metadata.Site metadata and web metadata fields
The following fields are needed in a site metadata record to implement the federation shown above.- server
- data directory path on the server
- pub directory path on the server
| Name | Server | DataDir | PubDir |
|---|---|---|---|
| am | strawman | /d/twiki/data | /d/twiki/pub |
| eu | woodenman | /var/twiki/data | /var/twiki/pub |
| as | tinman | /share/twiki/data | /share/twiki/pub |
- admin group
- master site
| Name | Admin | Master |
|---|---|---|
| WebOne | GodelGroup | am |
| WebTwo | EscherGroup | eu |
| WebThree | BachGroup | as |
How to get and put data - overview
- You can retrieve data from the metadata repository using %MDREPO{...}%.
- You can put data by the
mdreposcript. It works from browser as well as command line.
mdrepo script from command line
Go to the bin directory then you can use themdrepo script in the following format: ./mdrepo COMMAND ARGUMENT ...
Arguments depend on the command.
mdrepo show TABLE RECORD_ID
Shows the specified record of the specified table. Example:
$ ./mdrepo show sites am
am
datadir=/d/twiki/data
pubdir=/d/twiki/pub
server=strawman
mdrepo list TABLE
Shows all the records of the specified table. Example:
$ ./mdrepo list sites
am
datadir=/d/twiki/data
pubdir=/d/twiki/pub
server=strawman
as
datadir=/share/twiki/data
pubdir=/share/twiki/pub
server=tinman
eu
datadir=/var/twiki/data
pubdir=/var/twiki/pub
server=woodenman
mdrepo add TABLE RECORD_ID FIELD_NAME=VALUE ...
Adds a new record. It returns nothing. If the specified record already exists, it complains. Example:$ ./mdrepo add webs WebFour admin=HofstadterGroup master=am
mdrepo updt TABLE RECORD_ID FIELD_NAME=VALUE ...
Update an existing record. It returns nothing. If the specified record does not exist, it complains. Example:$ ./mdrepo updt webs WebFour admin=GardnerGroup master=am
mdrepo del TABLE RECORD_ID
Deletes an existing record. It returns nothing. If the specified record does not exist, it complains. Example:$ ./mdrepo del webs WebFour admin=GardnerGroup master=am
mdrep load TABLE FILE
Loads records to the specified table from the specified file. The file content is in the same format as the list command's output. Nonexistent records are created. Existing records are updated. Example:$ ./mdrepo load /var/tmp/temp-webs
mdrepo rset TABLE
Makes the specified table empty. It returns nothing. Example:$ ./mdrepo rset sites
mdrepo script from browser
Restrictions
Compared with command line use, using it from browser is restricted for risk mitigation.- Not all tables are subject to manipulation from brower. Only tables permitted by Configuration.
- The sites tabe is rarely updated hence allowing its updat from browser does not increase convenience significantly. Still, if it's modified in a wrong manner, the damage can be huge. So making it updatable from browser is not recommended.
- Only the following commands can be issued from browser:
add,updt,del-
showandlistcommands are not needed because %MDREPO{...}% does those jobs. -
loadandrsetare too dangerous.
-
mdrepo script is used from browser, %ALLOWROOTCHANGE% is examined. If it allows you, the operation is executed.
If %ALLOWROOTCHANGE% does not allow you, TWiki checks if the user mapping handler has the mdrepoOpAllowed() method.
If the method exists, it's called in the following manner to check if the operation is permitted.
$mapping->mdrepoOpAllowed($cUID, $cmd, $table, $recId, \%rec);Here's how
mdrepoOpAllow() is supposed to behave. - If the operation is allowed, the method returns "" (a null string), in which case the the operation is executed
- Otherwise, it returns the reason of not allowing, in which case, the operation is not executed
lib/TWiki/UI/MdrepoUI.pm about how exactly it's called and its result is used.
By providing mdrepoOpAllowed(), you can make metadata creation/update/deletion self-service to some extent.
But for mdrepoOpAllowed(), all metadata manipulation requires TWikiAdminGroup members' intervention.
URL parameters
mdrepo script checks - if the
_addparameter is true (a string other than "0" or "" (zero length string) - otherwise checks if the
_updtparameter is true - otherwise checks if
_delis true
_table and _recid parameters.
Field values are specified by parameters of the =__FIELD_NAME format.
For example, submitting the following form has the same effect as the command line shown further below.
<form action="%SCRIPTURL%/mdrepo" method="post"> <input type="hidden" name="_add" value="add"/> <input type="hidden" name="_table" value="webs"/> <input type="hidden" name="_recid" value="WebFour"/> <input type="hidden" name="__admin" value="GardnerGroup"/> <input type="hidden" name="__master" value="am"/> <input type="submit"/>
$ ./mdrepo add webs WebFour admin=GardnerGroup master=am
Output
By default, the script's output is in the text/plain MIME type. If the command succeeds, it returns nothing. When something goes wrong, an error message is returned. Ifredirectto URL parameter is provided, the script returns HTTP redirect to the specified URL.
If the redirectto parameter contains %RESULT%, it's replaced by the message to be shown when redirectto is not specified.
Record IDs and field names
So far, only metadata tables for sites and webs are discussed. TWiki core uses only those two tables. But the metadata repository can house more tables. For sites and webs tables, word characters (letters, numbers, and underscores(_)) are enough for record IDs. So by default, record IDs are restricted to those characters to avoid confusion and unnecessary complication. As described in the next section, you can specify a regular expression of valid record IDs. You may need to specify it if you use other tables than sites and webs. Similarly, field names are restricted. By default, field names are restricted to word characters. You can specify a regular expression of valid field names if needed.Configuration
To turn on the metadata repository, you need to have the following three settings.
$TWiki::cfg{Mdrepo}{Store} = 'DB_File';
$TWiki::cfg{Mdrepo}{Dir} = '/var/twiki/mdrepo';
$TWiki::cfg{Mdrepo}{Tables} = [qw(sites webs:b)];
- $TWiki::cfg{Mdrepo}{Store}
- Specifies a tie-able Perl class.
- $TWiki::cfg{Mdrepo}{Dir}
- Specifies a path to a directory where the MdrepoStore class have files.
- $TWiki::cfg{Mdrepo}{Tables}
- Specifies the names of the tables used. A table name may be followed by a colon and options. "b" is currently the only option recognized, which means the table can be updated from browser.
$TWiki::cfg{Mdrepo}{WebRecordRequired} = 1;
For a large site having thousands of webs, this is handy for site management.
Specifically this brings the following behaviors. - A web not having a web metadata record regarded as nonexistent. Existence of a directory under $TWiki::cfg{DataDir} isn't enough.
- A web creation by ManagingWebs is rejected if the corresponding web metadata is not present. Similarly, a web cannot be renamed to a web whose top level web doesn't have its web metadata record.
- %WEBLIST{...}% gets faster referring to web metadata rather than traversing a directory hiearchy. For practicality, only top level webs are listed except with the current web -- the current web's ancestors and decendants are listed.
$TWiki::cfg{Mdrepo}{RecordIDRe} = '\\w[-.:\\w]*';
$TWiki::cfg{Mdrepo}{FieldNameRe} = '\\w[-\\w]*';
Audit trail
When themdrepo script is used either from command line or browser, if the command is either add, updt, del, or rset, it's recorded on the log file in the same manner as other scripts. Specifically, the activity is put on the 5th column.
| Command | 5th column format |
|---|---|
add |
add TABLE RECORD_ID FIELD_NAME=VALUE ... |
updt |
cur TABLE RECORD_ID FIELD_NAME=VALUE ... |
del |
cur TABLE RECORD_ID FIELD_NAME=VALUE ... |
rset |
cur TABLE RECORD_ID FIELD_NAME=VALUE ... |
updt, del, and rset commands put multiple log entries so that the previous values are recorded. Here's an example of log entries left by a updt operation.
| 2012-06-15 - 13:16 | guest | mdrepo | TemporaryTestWeb.TestTopic | cur sites am datadir=/d/twiki/data pubdir=/d/twiki/pub server=strawman | | | 2012-06-15 - 13:16 | guest | mdrepo | TemporaryTestWeb.TestTopic | updt sites am datadir=/d/twiki/dat pubdir=/d/twiki/pu server=strawma | |When the
mdrepo script is used from a command line, the topic name on the log is always Main.WebHome.
Audit trail is there by default.
In case you want to suppress it, you can do it by setting a false value to $TWiki::cfg{Log}{mdrepo} configuration preference.
Related Topics: AdminDocumentationCategory, AutonomousWebs, ReadOnlyAndMirrorWebs, UsingMultipleDisks, UserMasquerading| I | Attachment | History | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|---|
| |
site-mirroring.png | r1 | manage | 16.2 K | 2012-06-14 - 01:50 | TWikiContributor |
This topic: TWiki > MetadataRepository
Topic revision: r2 - 2015-03-09 - TWikiContributor
Ideas, requests, problems regarding TWiki? Send feedback
Note: Please contribute updates to this topic on TWiki.org at TWiki:TWiki.MetadataRepository.

